
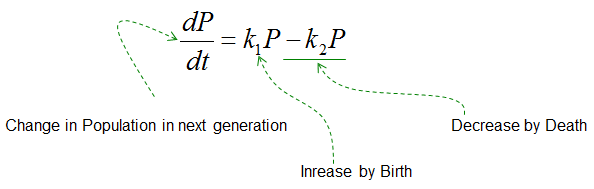
Modeling and predicting non-isothermal microbial growth using general purpose software. Since I am interested in how the changing parameters (due to changing temperature) lead to growth in the end, I would think I would need to integrate with respect to $T$? But I am unsure if this means solving the differential equations of the second-order parameters (because they are the only ones that directly have $T$ in them) or if that means doing something else to the primary equation?įor reference, the paper I am using most often is:Ĭorradini, M. I have little experience in differential equations and sadly, I am actually just not even sure which part of my model would need to be integrated. My trouble is that one paper specifying a different growth model (logistic) was able to model bacterial growth under ANY temperature regime you can think of by deriving a differential equation for their primary model. $$\log_=0.0421\cdot(T-12.0570),$$ where $T$ is temperature.Īll of the secondary models are dependent upon temperature, since bacteria obviously favor warmer conditions and grow faster, up to a certain point. Magnolia provides the tools for developing models using an equation-based modeling language, scripting the execution of simulations using either the Python programming language or a simple command-based language, and for interactively exploring model behavior using an intuitive. The primary growth model, using the modified Gompertz equation, is: Magnolia is an environment for modeling systems whose behavior can be described by systems of differential equations. I am working on building a growth model for bacteria for a risk assessment, and would like to move the growth model past static temperature conditions. I hope this is the right place for this question.


 0 kommentar(er)
0 kommentar(er)
